[백준 / C언어] 17070번: 파이프 옮기기 1 (dp, 다이나믹 프로그래밍)

https://www.acmicpc.net/problem/17070

17070번: 파이프 옮기기 1

 

난이도: solved.ac 골드 5

 

알고리즘 분류

---

다이나믹 프로그래밍 (dp), 그래프 탐색 (DFS)

 

접근 방법

---

각 칸 별로 옮길 수 있는 방법의 수가 정해져 있으므로 dp를 이용해 풀어야겠다고 생각했다.

파이프를 옮겼을 때 가로 상태이려면 이전 상태가 가로 또는 대각선 상태여야 한다.

그리고 대각선 상태라면 이전 상태가 가로 또는 대각선 또는 세로 상태여야 하고, 세로 상태라면 이전 상태가 대각선 또는 세로 상태여야 한다.

 

따라서 점화식은 아래와 같다.

가로 = 가로 + 대각선

대각선 = 가로 + 대각선 + 세로

세로 = 대각선 + 세로

(좌변: 현재 상태, 우변: 이전 상태)

 

위의 점화식을 이용해 dp 테이블을 만들었다.

그리고 이 dp 테이블에는 각 상태별(가로, 대각선, 세로) 파이프의 오른쪽 부분이 가리키는 경우의 수를 저장했다.

 

위의 그림처럼 옮긴 후의 파이프가 가로 상태라면 이전 상태가 가로 또는 대각선 상태여야 하는데, 이전 상태에서 파이프의 오른쪽 부분이 가리키는 좌표는 현재 좌표의 왼쪽 좌표이다.

옮긴 후의 파이프가 대각선 상태라면 이전 상태는 가로 또는 대각선 또는 세로 상태여야 하는데, 이전 상태에서 파이프의 오른쪽 부분이 가리키는 좌표는 현재 좌표의 왼쪽 위 좌표이다.

옮긴 후의 파이프가 세로 상태라면 이전 상태는 대각선 또는 세로 상태여야 하는데, 이전 상태에서 파이프의 오른쪽 부분이 가리키는 좌표는 현재 좌표의 바로 위 좌표이다.

 

아래는 입력으로

5

0 0 0 0 0

0 0 0 0 0

0 0 0 0 0

0 0 0 0 0

0 0 0 0 0

을 입력했을 때의 예시다. (벽이 하나도 없는 상태)

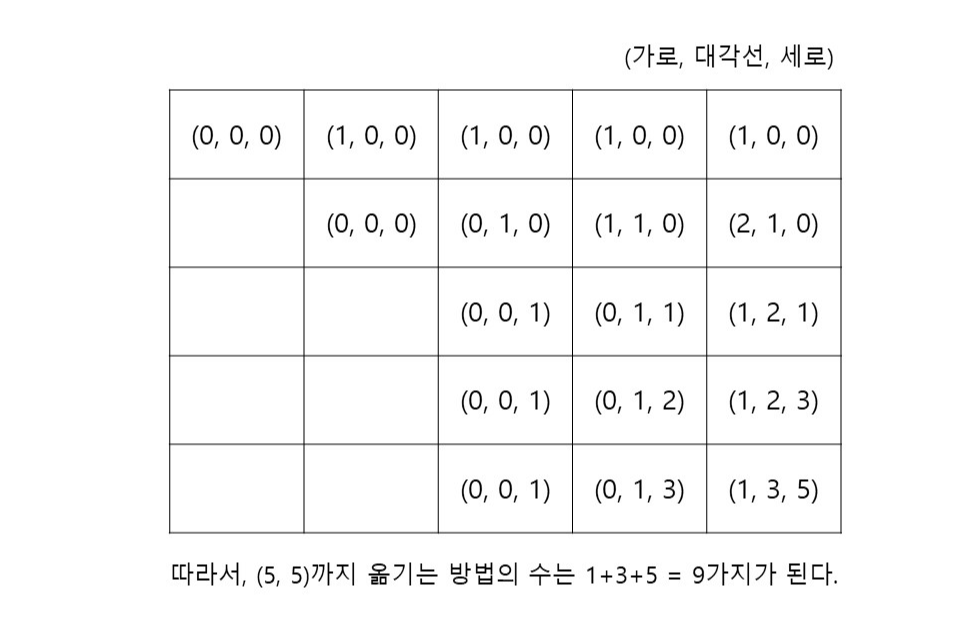
이해가 되었으려나...ㅎ

구현

---

먼저 2차원 배열 map으로 집의 상태를 입력받고, 2차원 구조체 배열 cases를 이용해 각 칸 별로 가로 상태로 옮길 수 있는 방법의 수, 대각선 상태로 옮길 수 있는 방법의 수, 세로 상태로 옮길 수 있는 방법의 수를 저장할 수 있도록 했다.

 

1행 부분은 이전 상태가 가로였을 때만 옮기는 게 가능하므로 가로 상태의 경우가 1이 되도록 (1, 0, 0) 로 초기화해 주었다.

단, 벽이 있다면 그 뒤로는 모두 옮기는 게 불가능하므로 그 뒷부분은 초기화해주지 않았다.

 

점화식으로 dp 테이블을 채워 넣을 때는 2행부터 채우도록 for문에서 i = 1부터 시작하게 해 주었고, 생각해 보면 1열과 2열로 옮길 수 있는 것은 불가능하므로 3열부터 (for문에서 j = 2) dp 테이블을 채우게 해 주었다.

 

코드

---

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>

typedef struct _Pipe {
	int horiz;	// 가로
	int diag;	// 대각선
	int verti;	// 세로
} pipe;

pipe cases[16][16];
int map[16][16];

int main() {
	int N, i, j;
	scanf("%d", &N);
	for (i = 0; i < N; i++)
		for (j = 0; j < N; j++)
			scanf("%d", &map[i][j]);
            
	// 1행은 가로로만 움직일 수 있으므로 1행의 가로 부분을 1로 초기화
	for (j = 0; j < N; j++) {
		if (map[0][j])	// 벽이 있으면 그 뒤부터는 못 가므로
			break;
		cases[0][j].horiz = 1;
	}

	for (i = 1; i < N; i++) {
		for (j = 2; j < N; j++) {
			// 움직이려는 곳이 벽이 아닐 때만
			if (!map[i][j]) {
				cases[i][j].horiz = cases[i][j - 1].horiz + cases[i][j - 1].diag;
				cases[i][j].verti = cases[i - 1][j].diag + cases[i - 1][j].verti;
				// 대각선으로 움직이려면 아래, 오른쪽까지 벽이 없어야 하므로
				if (!map[i][j - 1] && !map[i - 1][j - 1] && !map[i - 1][j])
					cases[i][j].diag = cases[i - 1][j - 1].horiz + cases[i - 1][j - 1].diag + cases[i - 1][j - 1].verti;
			}
		}
	}
	int sum = cases[N - 1][N - 1].horiz + cases[N - 1][N - 1].diag + cases[N - 1][N - 1].verti;
	printf("%d", sum);
	return 0;
}