[백준 / C언어] 11051번: 이항 계수 2 (파스칼의 삼각형)

https://www.acmicpc.net/problem/11051

11051번: 이항 계수 2

 

난이도: solved.ac 실버 2

 

 

앞에서 다룬 문제 (이항 계수 1)의 확장판(?)이다

 

N과 K의 범위가 1000까지로 늘어났다

 

이 문제는 파스칼의 삼각형을 이용하면 쉽게 풀 수 있다

 

파스칼의 삼각형의 공식을 dp 점화식으로 만드는 건데, 이에 대해 설명해 보겠다

 

우선 파스칼의 삼각형은 아래와 같다

 

 

출처: 파스칼의 삼각형 - 위키백과

 

이 파스칼의 삼각형은 아래의 이항계수로부터 만들어진 건데

 

출처: wikimedia commons

 

각 수는 한 칸 왼쪽 위와 한 칸 오른쪽 위의 수의 합이라는 특징이 있다

 

이를 수식으로 나타내면 다음과 같다

 

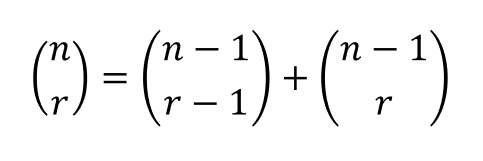
근데 이 식을 설명하는 이유가 뭘까?

 

우선 dp는 큰 문제를 작은 문제로 나누어 푸는 거라는 걸 알아야 한다

 

이항계수는 위의 파스칼의 삼각형에서 보이는 것처럼 조합(combination)으로 표현할 수 있는데

 

조합은 유한 개의 원소에서 주어진 수만큼의 원소를 선택하는 경우의 수를 말한다

 

예를 들어 5개의 숫자에서 3개를 선택하는 경우의 수를 구해야 한다고 해보자

 

이는 아래처럼 나타낼 수 있다

 

 

사실 이 경우의 수는 이전 문제에서 보인 조합 공식에 넣으면 바로 구할 수 있지만, 다이나믹 프로그래밍 방법으로 구해보자

 

이 문제는 작은 문제로 쪼갤 수 있다

 

5개의 숫자를 하나하나 보며 선택할지 말지를 결정한다고 하면

 

마지막으로 택하는 숫자를 결정하는 건 이전의 4개의 숫자를 어떻게 고르느냐에 따라 달라진다

 

이전의 4개의 숫자에서 이미 3개를 다 골라놓았다면 마지막의 숫자는 선택하지 않게 되고, 2개를 골라놓았다면 마지막 숫자는 무조건 선택하게 된다

 

다시 말하면, 5개의 숫자에서 3개를 선택하는 경우의 수는 4개의 숫자에서 3개를 고르는 경우의 수와 4개의 숫자에서 2개를 고르는 경우의 수로 나눌 수 있다

 

 

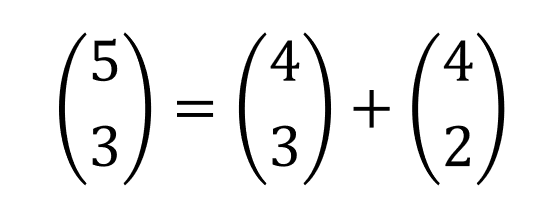
그리고 이를 일반화하여 표현한 게 바로 위에서 보인 이 식이다

 

이를 dp 점화식으로 나타내면 아래와 같다

 

dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]

 

dp[i][j]는 i개의 숫자 중 j를 선택하는 경우의 수를 말한다

 

이 점화식을 그대로 코드로 옮기면 아래와 같이 된다

 

#include<stdio.h>
#include<stdlib.h>

int main() {
	int N, K, i, j;
	scanf("%d %d", &N, &K);
    
	int** dp = (int**)calloc(N + 1, sizeof(int*));
	for (i = 0; i < N + 1; i++)
		dp[i] = (int*)calloc(N + 1, sizeof(int));
        
	for (i = 1; i <= N; i++) {
		dp[i][0] = 1;	// (n, 0) = 1
		dp[i][i] = 1;	// (n, n) = 1
		dp[i][1] = i;	// (n, 1) = 1
	}
    
	for (i = 3; i <= N; i++) {
		for (j = 2; j < i && j <= K; j++)
			dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j]) % 10007;
	}
    
	printf("%d", dp[N][K]);
    
	for (i = 0; i < N; i++)
		free(dp[i]);
	free(dp);
	return 0;
}

 

이중 for문에서 i가 3부터 시작하는 이유는

 

바로 위의 for문이 끝나면 아래의 테이블처럼 index 2까지는 값이 채워져 있기 때문이다 (나머지 빈칸은 calloc으로 동적할당했기 때문에 0으로 채워져 있다)